Nessas últimas semanas fizemos algumas experiências de física vinculadas à disciplina MAC0209 – Modelagem e Simulação do Instituto de Matemática e Estatística da Universidade de São Paulo (IME-USP). Esse post fala um pouco sobre essas experiências.
Foram um total de 4 experiências:
- Realização de um movimento retilíneo uniforme (MRU)
- Realização de um movimento retilíneo uniformemente variado (MRUV)
- Realização de um movimento pendular
- Realização de um movimento de descida sobre um plano inclinado / rampa
Em cada uma dessas experiências nosso objetivo era mensurar / coletar dados experimentais de posição em relação ao tempo do objeto foco do experimento. Por exemplo, para o experimento de MRU queríamos mensurar a posição de um carrinho em um determinado instante de tempo. A partir desses dados experimentais eram então estimadas outras medidas experimentais, por exemplo a velocidade do carrinho no instante t. Em seguida comparamos os resultados experimentais com resultados obtidos por modelos matemáticos que descrevem os movimentos de interesse ou então com aproximações obtidas por métodos numéricos, a fim de criar uma discussão sobre a qualidade de se aproximar matematicamente movimentos reais por esses modelos e/ou métodos.
Movimento Retilíneo Uniforme (MRU) e Movimento Retilíneo Uniformemente Variado (MRUV)
Construimos um carrinho controlado por bluetooth de maneira que fosse possível controlar sua direção e também sua velocidade (Figura 1). O carrinho foi feito a partir de um antigo brinquedo de rádio doado para o grupo Hardware Livre USP. Ele é formado por três componentes: LD293 (ponte H) circuito integrado para controlar os motores, módulo bluetooth (HC05) e Arduino pro mini (descrição mais detalhada aqui.
Para marcar o tempo ao invés de cronômetros foi utilizado o relógio interno do microcontrolador da placa ArduinoUNO. Para detectar quando o carrinho passou por certo ponto foram utilizados quatro sensores de luminosidade do tipo LDR (Light Dependent Resistor) (Figura 2). No carrinho colocamos um celular com um aplicativo PhysicsToolBoxSuite para medir o acelerômetro interno do celular e uma pequena lanterna de modo que ao passar do lado do sensor esse seria ativado e mandaria um sinal para ArduinoUNO, que por sua vez enviaria o tempo percorrido para serial do computador (Figura 3). O percurso total percorrido pelo carrinho em cada um dos experimentos foi de 6 metros (Figura 4). Assim, quando o carrinho passa pelo o LDR 1, o cronômetro do microcontrolador começa e para cada ponto é enviado o tempo para computador.




Segue um vídeo mostrando o funcionamento do experimento que também pode ser visto no canal da disciplina.
Pêndulo
Para os experimentos pendulares utilizamos um pêndulo de madeira cuja haste media aproximadamente 65 centímetros do seu ponto de rotação até o seu ponto mais distante (Figura 5). Usamos também uma ArduinoUNO junto com um sensor ultrassônico HC-SR04 e medimos a distância da ponta do pêndulo ao sensor (que ficou preso a uma parede) em vários instantes de tempo e de forma contínua de modo que pudéssemos obter a posição experimental xe(t) do pêndulo ao longo de todo o experimento (Figura 6). Usamos também um celular acoplado ao pêndulo para medir o ângulo inicial dos experimentos.


Descida sobre plano inclinado / rampa
Os experimentos de descida sobre plano inclinado foram realizados com um cano de PVC de 3 metros de comprimento ao longo do qual foram acoplados 11 sensores de luminosidade (do tipo LDR) em pontos equiespaçados (Figura 7). Os sensores ficaram posicionados no “topo” do cano (Figura 8) e, por dentro do cano, debaixo deles passamos um carrinho com uma lanterna focalizada (Figura 9) que iluminava cada um deles no instante de sua passagem. Usamos então as leituras dos sensores e uma ArduinoMEGA para marcar em que instante de tempo o carrinho passava por cada um dos pontos xe ao longo do cano. Também usamos um celular acoplado à rampa para medir o ângulo inicial dos experimentos.



Segue um vídeo mostrando o funcionamento dos experimentos com o pêndulo e com a rampa que também pode ser visto no canal da disciplina.
Os programas Arduino utilizados para realizar os experimentos estão disponíveis no GitHub.
Resultados Obtidos
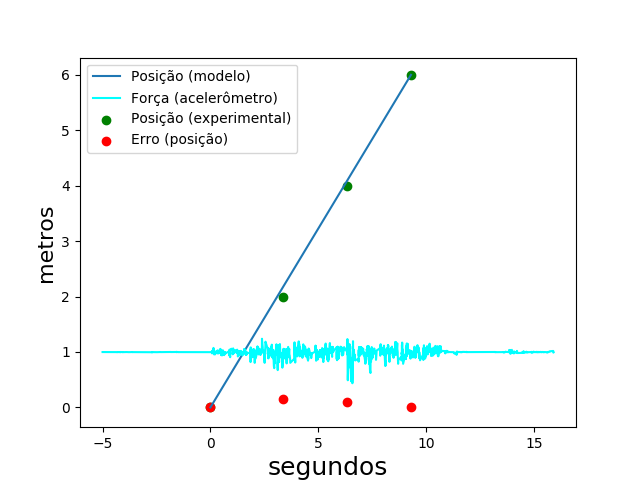
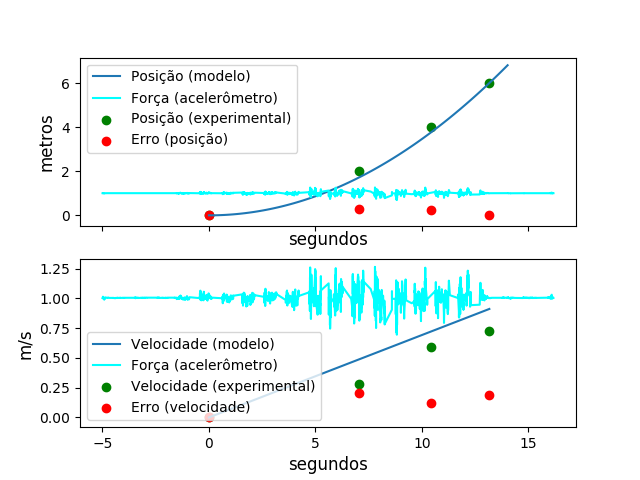
Seguem os resultados obtidos com os experimentos de MRU e MRUV (Figuras 10 e 11).
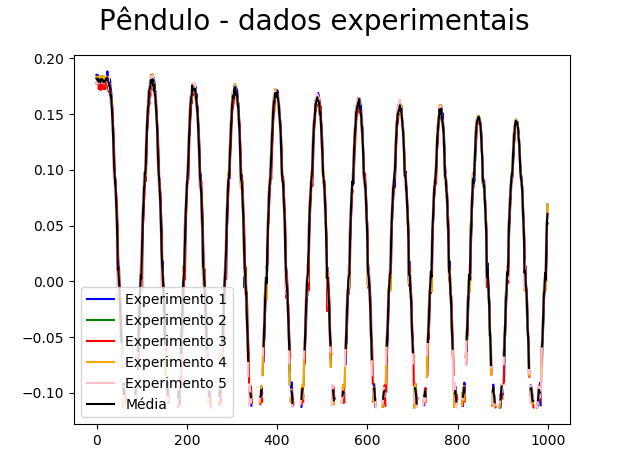
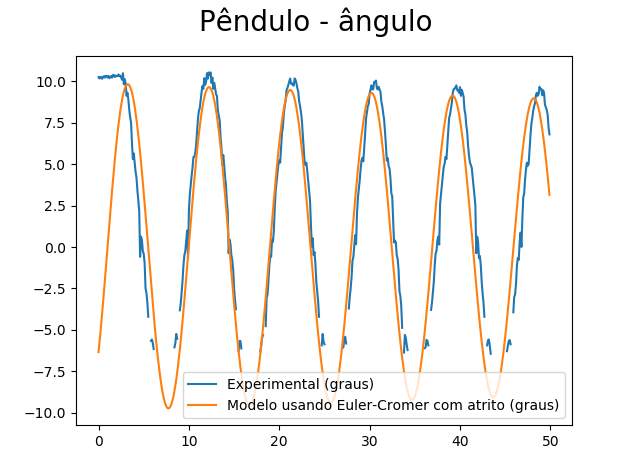
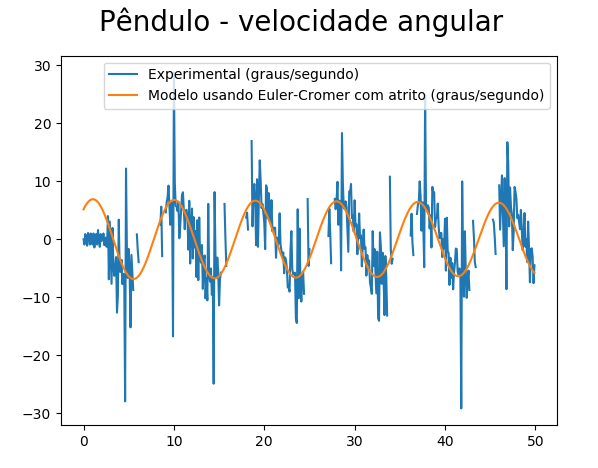
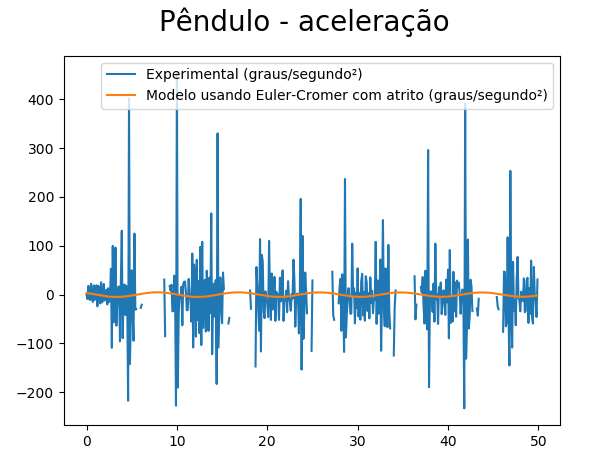
Seguem agora os resulatados obtidos com os experimentos de pêndulo (Figuras 12 a 15). Essencialmente se tratam de um gráfico contendo as medidas dos ângulos experimentais ao longo do tempo para 5 experimentos junto com o ângulo médio dos experimentos (Figura 12). Em seguida temos os gráficos de ângulo ao longo do tempo (Figura 13), velocidade angular ao longo do tempo (Figura 14), e aceleração angular ao longo do tempo (Figura 15) comparando dados experimentais do experimento número 5 com as respectivas medidas calculadas numéricamente usando os métodos de Euler-Cromer (com atrito), Euler-Cromer (sem atrito) e Euler (sem atrito).
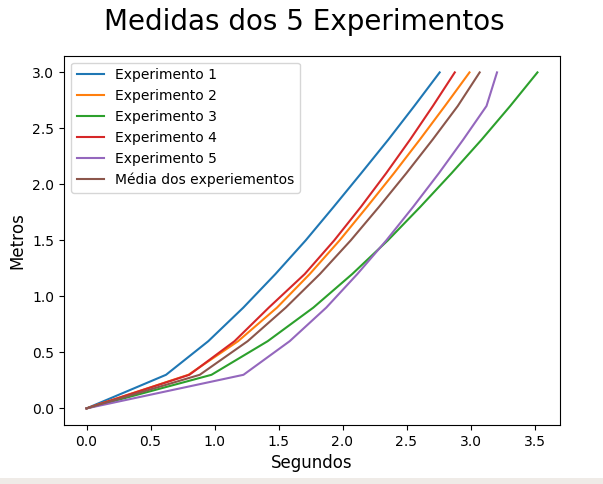
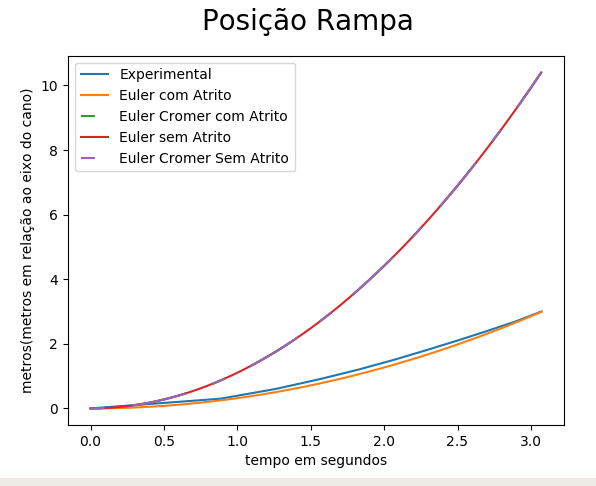
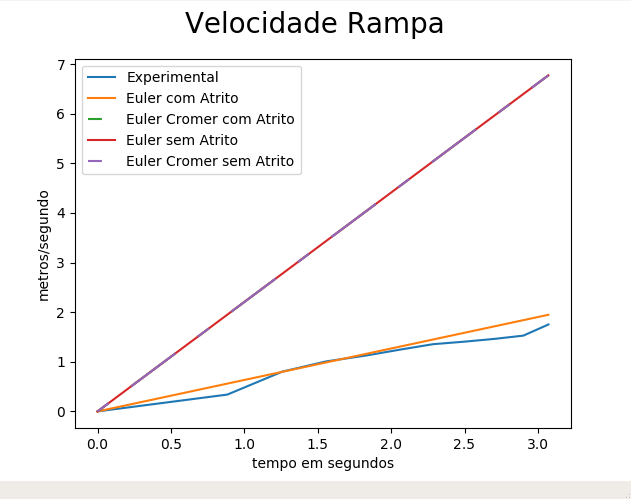
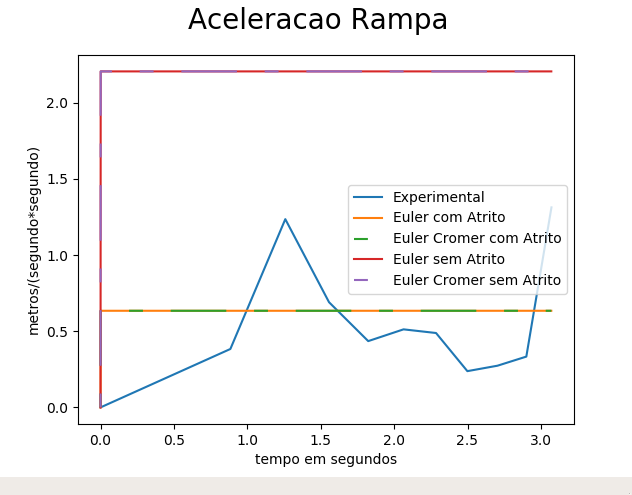
Por fim temos os resultados obtidos com os experimentos de descida sobre plano inclinado / rampa (Figuras 16 a 19) que consistem nos gráfico contendo as medidas dos posições experimentais ao longo do tempo para os 5 experimentos junto com a posição média dos experimentos (Figura 16) seguidos dos gráficos de posição ao longo do tempo (Figura 17), velocidade ao longo do tempo (Figura 18), e aceleração ao longo do tempo (Figura 19) comparando dados experimentais do experimento de número 5 com as respectivas medidas calculadas numéricamente usando os métodos de Euler-Cromer (com atrito), Euler-Cromer (sem atrito), Euler (com atrito), e Euler (sem atrito).
Interpretação e Conclusão
Em relação às experiências de MRU e MRUV, pela forma como os experimentos foram conduzidos, perceberam-se interferências na forma de atrito (seja entre o carrinho e o chão, entre o carrinho e outros objetos presentes no ambiente do experimento ou mesmo entre as próprias partes do carrinho) o que fez os experimentos divergirem um pouco do seu modelo teórico proposto. Para o MRU notamos que essas forças de atrito podem ser relevadas uma vez que se consiga evitar que elas variem muito ao longo da trajetória e que se consiga aplicar uma força constante (e empiricamente de mesma magnitude que as forças de atrito) sobre o carrinho. Para o MRUV também vale a ideia de minimizar e manter constantes as forças de atrito embora seja mais difícil conseguir isso aplicando força de modo a acelerar o carrinho.
Em relação às experiências com o pêndulo foram realizados testes com métodos numéricos ideais e métodos numéricos que consideram atrito. Percebeu-se que ambas as aproximações eram razoáveis para um curto intervalo de tempo a partir do começo do experimento mas que, eventualmente, ficam com erro considerável porque o pêndulo real fica fora de fase em relação ao pêndulo do modelo. Isso ocorre porque a posição é muito sensível às constantes físicas relativas ao atrito. Apesar disso, o método com atrito aproxima de forma muito mais eficiente o experimento porque seu erro não aumenta muito ao longo do tempo enquanto erro do método ideal aumenta drasticamente ao longo do tempo do experimento. Outra conclusão é que o método numérico com atrito aproxima de forma muito melhor a energia do sistema (a amplitude do pêndulo diminui ao longo do tempo assim como ocorre experimentalmente).
Em relação às experiências de descida sobre plano inclinado / rampa concluímos que, para simular a descida de um objeto (carrinho) sobre um plano inclinado (rampa), os métodos numéricos ideais (que não consideram forças de atrito) não são bons para estimar as variáveis do sistema, seja posição, velocidade ou aceleração. Por outro lado os métodos que consideram que o sistema possui resistência são muito mais eficázes. De fato é razoável aproximar as variáveis do sistema (descida na rampa) por métodos numéricos que consideram resistência porque eles conseguem se adequar ao fato do movimento real ser amortecido. Não podemos dizer o mesmo sobre a aproximação com métodos ideais.
Agradecimentos Especiais:
- Leonardo Daneu: Por auxiliar na filmagem dos experimentos de MRU e MRUV.
- Lucas Sung Jun Hong: Por auxiliar na filmagem dos experimentos e na edição dos vídeos de MRU e MRUV.
- Roberto Hirata Junior: Por emprestar o pêndulo, o cano que serviu de rampa para os experimentos, a ArduinoMEGA, e os sensores de luminosidade utilizados na rampa.
- Dario Vargas: Pela filmagem de um dos experimentos de pêndulo.
- Grupo Hardware Livre USP: Por ceder ferramentas e componentes para a montagem dos experimentos.
Este trabalho não teria ficado tão completo sem a ajuda de vocês. Muito Obrigado!